Disney “principled” BRDF [1] is a very interesting shading model. It can achieve various physically plausible appearances with only one color parameter and ten scalar parameters! This shading model is designed not only to catch most of the measured data from MERL, but also to follow the principles below:

Intuitive rather than physical.
As few parameters as possible.
Parameters are zero to one over their plausible range.
Parameters are allowed to be pushed beyond their plausible range where it makes sense.
All combinations of parameters should be as robust and plausible as possible.

These art-directable features make artists achieve the desired shading results more easily, it is one of the ultimate goals for software engineering in animation studio. Therefore, it has been implemented within various frameworks like Unreal Engine 4, RenderMan, MPC’s preview system Dekko, etc. So, let’s make one for Arnold. :)

Importance Sampling

According to the source code from BRDF explorer, the shading components of Disney BRDF can be separated into two parts:

diffuse
- base diffuse
- Hanrahan-Krueger subsurface
specular
- primary specular (anisotropic GTR2)
- clearcoat (GTR1)
- sheen

Diffuse

From BRDF explorer, we can see that the diffuse component is dominated by the $\cos{\theta_l}$ factor. Thus the diffuse part could be sampled with the PDF proportional to cosine-weighted solid angle: diffuse sample distribution

Specular

Sheen is relatively small to primary specular (GTR2) and clearcoat (GTR1) and it is ignored in the importance sampling process in current implementation. The importance sampling approach for GTR is pretty much like we did for GGX previously, except for the anisotropic case which is a little complicated (I’ve not successfully derived the formula yet). Fortunately, Burley has kindly provided the details in the course notes [1], and we could simply follow those formulas to generate samples:

$$\begin{aligned} aspect &= \sqrt{1 - 0.9 \times anisotropic} \\ \alpha_x &= \frac{roughness^2}{aspect} \\ \alpha_y &= roughness^2 \times aspect \end{aligned}$$

For primary anisotropic specular:

$$\begin{aligned} D_{GTR_{2aniso}} &= \frac{1}{\pi}\frac{1}{\alpha_x\alpha_y}\frac{1}{(\sin^2{\theta_h}(\frac{\cos^2{\phi_h}}{\alpha_x^2}+\frac{\sin^2{\phi_h}}{\alpha_y^2})+\cos^2{\theta_h})^2} \\ h' &= \sqrt{\frac{\xi_2}{1-\xi_2}}[\alpha_x\cos(2\pi\xi_1)\vec{u}+\alpha_y\sin(2\pi\xi_1)\vec{v}]+\vec{n} \\ h &= \frac{h'}{|h'|} \end{aligned}$$

For clearcoat:

$$\begin{aligned} D_{GTR_1} &= \frac{\alpha^2 - 1}{\pi \log \alpha^2} \frac{1}{(1+(\alpha^2 -1)\cos^2\theta_h)} \\ \cos\theta_h &= \sqrt{\frac{1 - (\alpha^2)^{1 - \xi_2}}{1 - \alpha^2}},\ \phi_h=2\pi\xi_1 \end{aligned}$$

The microfacet normal $h$ is generated according to $D(\theta_h)\cos\theta_h$ which is already normalized over the hemisphere. Therefore, I tried to use the coefficents of $D_{GTR_2}, D_{GTR_1}$ as weights for lobe selection and PDF composition:

AtVector    sampleSpecularDirection(float rx, float ry) const
{
    // Select lobe by the relative weights.
    // Sample the microfacet normal first, then compute the reflect direction.
    AtVector M;

    float gtr2Weight = 1.0f / (mClearcoat + 1.0f);

    if (rx < gtr2Weight) {
        rx /= gtr2Weight;
        M = sampleGTR2AnisoDirection(rx, ry);
    } else {
        rx = (rx - gtr2Weight) / (1.0f - gtr2Weight);
        M = sampleGTR1Direction(rx, ry);
    }

    if (AiV3Dot(mAxisN, M) < 0.0f) {
        return AI_V3_ZERO;
    }

    return getReflectDirection(mViewDir, M);
}

float   evalSpecularPdf(const AtVector &i) const
{
    auto m = AiV3Normalize(i + mViewDir);
    auto IdotM = ABS(AiV3Dot(i, m));
    auto MdotN = AiV3Dot(m, mAxisN);

    if (MdotN < 0.0f) {
        return 0.0f;
    }

    float MdotN2 = SQR(MdotN);

    auto clearcoatWeight = mClearcoat / (mClearcoat + 1.0f);
    auto D = LERP(clearcoatWeight, D_GTR2Aniso(m, MdotN2), D_GTR1(m, MdotN2));
    return D * ABS(MdotN) * 0.25f / IdotM;
}

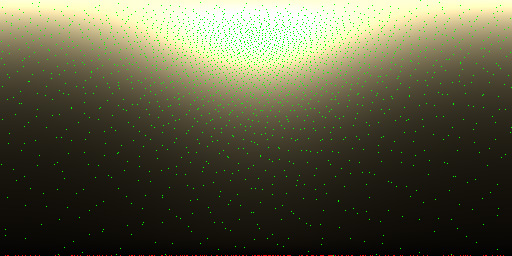
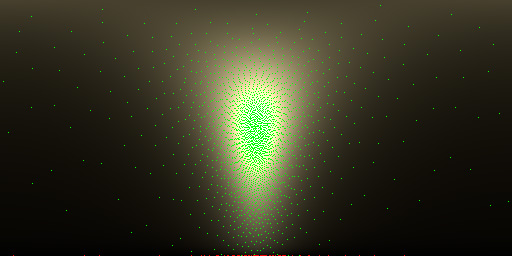
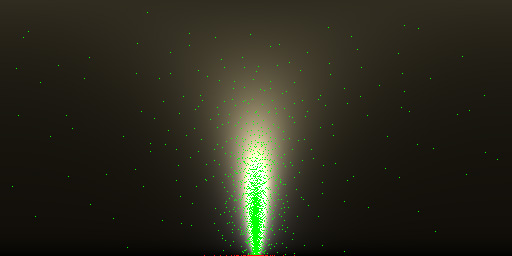
The red dots at bottom represent the invalid sample whose $\theta_m$ is greater than 90 degrees (i.e. $m \cdot n < 0$). It might be able to get improved by importance sampling the visible microfacet normals presented in Heitz and d’Eon [3].

Removing Fireflies

Current shading model is not energy conserved, sometimes the specular part would cause fireflies in indirect diffuse pass. The noise level can be reduced by using metallic parameter to blend the diffuse and GTR parts, but it would lost the clearcoating effect for non-metal material. Another possible approach is to skip specular evaluation for indirect ray samples (i.e. AI_RAY_DIFFUSE/AI_RAY_GLOSSY) like tutorial does with the price of missing reflection of metallic material.

indirect lighting

After few trial and errors, I found the most intuitive way is to use extra weights to scale the diffuse/specular radiance for indirect ray samples:

if (sg->Rt & (AI_RAY_DIFFUSE | AI_RAY_GLOSSY)) {
    diffuse *= AiShaderEvalParamFlt(p_indirect_diffuse);
    specular *= AiShaderEvalParamFlt(p_indirect_specular);
}

Results

The source code could be found here. If you have any idea or find any bug, please let me know in the comments.

References

Burley, Brent. "Physically Shading in Disney. 3/e." SIGGRAPH 2012 Course Notes. [source code]
Walter, Bruce, et al. “Microfacet models for refraction through rough surfaces.” EGSR'07.
Heitz, Eric, and Eugene d’Eon. “Importance Sampling Microfacet‐Based BSDFs using the Distribution of Visible Normals.” EGSR'14. [slides]