I have been using DSLR for over 10 years, I thought I knew few knowledge about photography. But after I watched a wonderful online course of digital photography by Prof. Marc Levoy [1], I just found there were so many details I weren’t aware before. The thing embarrassed me the most was that I incorrectly related f-number to lens aperture size. This post is trying to introduce the idea of f-number starting from scene radiance.

Radiance Invariance

Radiance [5] is a very important quantity in light transport. It is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit projected area per unit solid angle. In other words, it measures the density of photons passing near a position \(\mathbf{x}\) and travelling in directions in \(\omega\):

$$L(\mathbf{x}, \omega) = \frac{d^2 \Phi}{d\omega dA \cos{\theta}}$$

Radiance is invariant as it propagates along a line in empty space. That is, for two patches x, y in empty space, the radiance measured from x to y is identical to the one from y to x. This could be derived from the conservation of flux

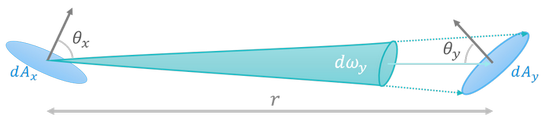
The radiance from y to x is

$$L_{y\rightarrow x} = \frac{d^2 \Phi}{\textcolor{#1eb8c1}{d\omega_y} dA_x \cos{\theta_x}} = \frac{\textcolor{#1eb8c1}{r^2}d^2 \Phi}{\textcolor{#1eb8c1}{dA_y\cos{\theta_y}} dA_x \cos{\theta_x}}$$

where \(d\omega_y = \frac{dA_y \cos{\theta_y}}{r^2}\). Likewise, the radiance from x to y is

$$L_{x\rightarrow y} = \frac{d^2 \Phi}{d\omega_x dA_y \cos{\theta_y}} = \frac{r^2 d^2 \Phi}{dA_x \cos{\theta_x} dA_y \cos{\theta_y}} = L_{y\rightarrow x}$$

This shows that the radiance interchanged between two patches is the same. But when the patch y goes farther at the distance \(r^\prime\) away from x, the solid angle \(d\omega_y^\prime\) would become \(\frac{r^2}{r^{\prime2}} d\omega_y\)

$$L^\prime_{y\rightarrow x} = \frac{d^2 \Phi^\prime}{d\omega^\prime_y dA_x \cos{\theta_x}} = \frac{d^2 \Phi^\prime}{d\omega_y dA_x \cos{\theta_x}} \frac{r^{\prime2}}{r^2}$$

From the inverse square law [7], the density of flux is inversely proportional to the square of the distance in between \(\Phi^\prime = \frac{r^2}{r^{\prime2}} \Phi\), therefore

$$L^\prime_{y\rightarrow x} = \frac{d^2 \textcolor{#1eb8c1}{\Phi^\prime}}{d\omega_y dA_x \cos{\theta_x}} \frac{r^{\prime2}}{r^2} = \frac{d^2 \textcolor{#1eb8c1}{\Phi}}{d\omega_y dA_x \cos{\theta_x}} \cancel{\frac{r^{\prime2}}{r^2}} \cancel{\textcolor{#1eb8c1}{\frac{r^2}{r^{\prime2}}}} = L_{y\rightarrow x}$$

Surprisingly, no matter how far the two patches are apart, the radiance is also constant as they moving along the same line. These two cases demonstrate the invariance of radiance.

Scene Radiance to Image Irradiance

Now, let’s consider a radiance transport from surface patch \(dA_o\) through a thin convex lens whose diameter is \(D\) onto the image patch \(dA_i\).

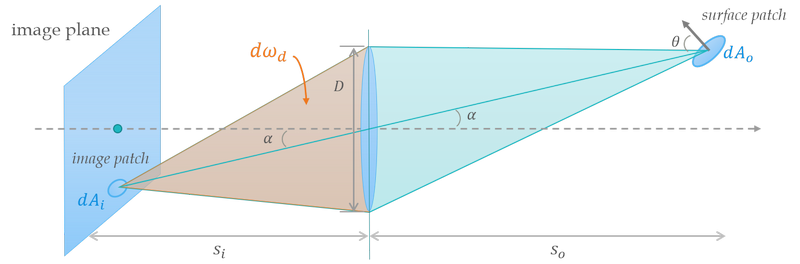
Suppose both surface patch and image plane are in the air (i.e. the refractive index is \(\approx 1\)). The irradiance of image patch is \(E_i = L_d\ d\omega_d \cos{\alpha}\), where \(L_d\) is the radiance from lens to \(dA_i\) in directions \(d\omega_d\). Since all radiances from the patch \(dA_o\) through the thin convex lens would converge on the image patch \(dA_i\), and with the radiance invariance property, we could associate the radiance from surface patch to image patch \(L_d = L_o\). Therefore

$$E_i = L_d \frac{\pi(\frac{D}{2})^2 \cos{\alpha}}{(\frac{s_i}{\cos{\alpha}})^2} \cos{\alpha} = L_o \frac{\pi}{4} \Big(\frac{D}{s_i}\Big)^2 \cos^4{\alpha}$$

This shows the image irradiance \(E_i\) is in linear proportion to scene radiance \(L_o\), and the factor \(\cos^4{\alpha}\) is the cause of vignette. To relate with lens focal length \(f\), \(s_i\) could be substituted by \(\frac{f s_o}{s_o - f}\) from Gaussian lens formula:

$$\frac{1}{f} = \frac{1}{s_i} + \frac{1}{s_o} \Rightarrow s_i = \frac{f s_o}{s_o - f}$$

Thus the fundamental radiometric relation between the scene radiance \(L_o\) and the irradiance \(E_i\) on image plane is

$$E_i = L_d \frac{\pi}{4} \Big(\frac{(s_o - f)D}{f s_o}\Big)^2 \cos^4{\alpha}$$

Be careful about the differences whether the focus is at infinity or not. By definition, the focal point is the converge point of parallel rays.

If the surface patch and image plane are in different medium, we should take the refractive index of both space into account. For more details, please refer to “Fundamental optical formulae” by Andy Rowlands [2].

Here we could see the image irradiance \(E_i\) changes w.r.t. focal length \(f\). It surprised me a lot, since I haven’t noticed the changes of exposure when I changed the focal length of a zoom lens. What’s happened underneath?

f-number

When focus is set at infinity (i.e. \(s_i \approx f, s_o = \infty\)), the irradiance \(E_i\) on image plane is

$$E_i = L_d \frac{\pi}{4} \Big(\frac{D}{f}\Big)^2 \cos^4{\alpha}$$

To make such relation numerically convenient, f-number \(N\) is defined as the ratio of focal length to the diameter of the aperture:

$$N = \frac{f}{D}$$

This means, for f/2.0 (i.e. \(N=2\)) lens, the aperture size is 25mm when the focal length is 50mm; while the aperture size is 50mm as the focal length is changed to 100mm. Additionally, the aperture size is

$$D = \frac{f}{N}$$

If \(f\) is fixed, doubling \(N\) would halve the size of aperture, therefore the exposure would reduce to 1/4 (\(N^\prime = 2N \rightarrow D^\prime = D/2 \rightarrow E^\prime = E/4\)). Likewise, if we want to double the exposure, we have to increase \(N\) by \(\sqrt{2}\). This is why the sequence of \(N\) is

$$1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, 32, …$$

When the focus is not at infinity, the apertal ratio \(\frac{(s_o - f)D}{f s_o}\) is called working f-number. For any fixed f-number, the aperture size would change along with the lens focal length. Therefore, the exposure is nearly constant with camera zoom.

Conclusion

I had accidentally mixed the definitions of aperture and f-number for a long time. The most embarrassing thing is that I’ve never noticed the difference of them myself, and spread my incorrect knowledge to people around me. I should study more thoroughly and should not take everything for granted. Always be aware of the knowledge gaps and review fundamental things more often to see if I have misunderstood something.

As always, if there are any mistakes in this post, please let me know. Thanks for your reading.

References

1. Marc Levoy. Lectures on Digital Photography, 2016.
2. Andy Rowlands. Fundamental optical formulae, 2017.
3. John P. Hess. The Properties of Camera Lenses, Filmmaker IQ.
4. CS6475. Computational Photography, Georgia Tech.
5. Wikipedia. Radiance.
6. Wikipedia. f-number.
7. Wikipedia. Inverse square law.